【機械学習＋外挿】機械学習モデルで外挿してみた

こんばんは。今日も機械学習を使った実験です。一般に機械学習は内挿は得意ですが外挿は苦手だと言います。というわけで、sin関数の一部を学習させ、外挿するとどうなるのかを実験して確かめることにしました。予測誤差を出力できるガウス過程回帰に加えて、機械学習３兄弟である（と勝手に思っている）ニューラルネットワーク、サポートベクターマシン、ランダムフォレストを用いて検証しました。問題設定としては、[0, 2pi] の範囲で学習を行い、それより３倍長い[0, 6pi]の範囲での予測を行いました。
〈お断り〉
scikitlearnとkerasモジュールを使いましたが、モデルのハイパーパラメータは学習データに出来るだけ適合するように選んでいます。一般にそんなパラメータは使わないよ、と思われることがあるかもしれませんが、どうかご容赦下さい。
〈目次〉
目次はこちら。最後に本稿のまとめを書きました。要するに、外挿するときは注意せよ、ということです。

ガウス過程回帰
ニューラルネットワーク
サポートベクター回帰
ランダムフォレスト
まとめ

ガウス過程回帰

まずはガウス過程回帰（GRP）からです。標準偏差を評価してくれるので大好きな手法です。GRPでは「カーネル」によってデータ同士の共分散を表現する必要がありますが、ここではRBF(Radial-basis function)カーネルを用いました（詳細はこちらの資料などをご参照下さい）。

ガウス過程と機械学習 (機械学習プロフェッショナルシリーズ)

作者:持橋大地,大羽成征
発売日: 2019/03/09
メディア: 単行本（ソフトカバー）

学習データ（赤点）は見事に再現できていますね！そして問題となる外挿領域（青線）ですが、２つ目の山を越えたあたりから全く予測できていません。また学習点がないことから信頼区間も大幅に広い範囲になっています。[0, 2pi]の範囲で学習できたからと言って永遠に波打つわけではないのですね。これは面白い。

f:id:Dajiro:20200421220944p:plain — ＧＰによるガウス過程回帰を用いた外挿。まったく予測できていない。

しかしながら、本来カーネルは解析対象となるデータの特徴に応じて適切に設計する必要があります。RBFは滑らかな関数のモデリングには向いていますが、sin関数のような周期的な関数に対しては、以下のExp-Sine-Squaredカーネルを使うべきでしょう。

Exp-Sine-Squaredカーネル： $\rm{exp}(-2($ $\rm{sin}$ $(\frac{\pi}{p}*d(xi, xj))/l)^{2}$ $)$

lは長さスケールを調整するためのハイパーパラメータで、pは周期性を調整するためのハイパーパラメータです。これらは最尤推定によって自動的に計算されますが、初期値や取りうる値の上限・下限を設定することができます。

このカーネルを用いてモデリングをすると以下のようになります。2piという周期性を上手く再現できていることが分かりますね。sin関数を使ってるので答えありきですし予測対象が単純すぎるきらいはありますが、適切なカーネルを選ぶことで結果はこれだけ変わるのだということがはっきり示されたのではないでしょうか。一番人気はRBFカーネルですが、色々なカーネルを知っておくのはGRPを使う上では必須だと言えると思います。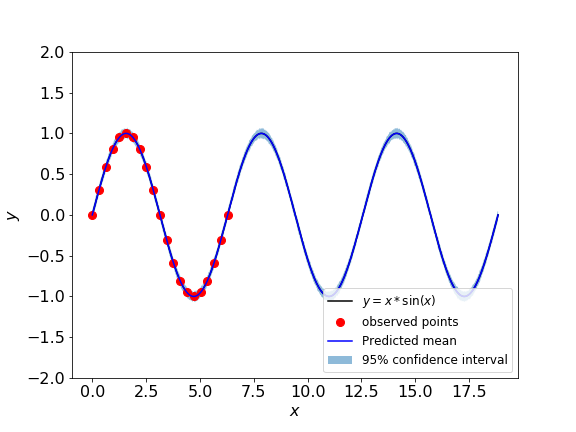

f:id:Dajiro:20200428103919p:plain — Exp-Sine-Squareカーネルによるフィッティングと外挿。

こちら、コードの一部です。周期性パラメータpの初期値は3.5としたのですが、自動的にp = 6.28(つまり2pi)に調整されたことが分かります。なお、初期値の取り方によって結果が大きく変わることには注意が必要です。結果が時々収束しません。

from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.gaussian_process.kernels import ConstantKernel, RBF, WhiteKernel, ExpSineSquared
from sklearn.preprocessing import StandardScaler

# GPモデルの構築
kernel = 1.0 * ExpSineSquared(1.0, 3.5, length_scale_bounds=(1e-05, 1.0e2), periodicity_bounds=(1e-1, 1.0e2)) + WhiteKernel()
gpr = GaussianProcessRegressor(kernel=kernel, alpha=0)
gpr.fit(X, scaler_y.transform(y))

print(gpr.kernel_)
#65.9**2 * ExpSineSquared(length_scale=100, periodicity=6.28) + WhiteKernel(noise_level=1e-05)

ニューラルネットワーク

お馴染み、ニューラルネットワークの結果がこちらです。2piまではほぼ完全に学習できていますが、即座にsin関数から離れていってしましました。GPでは２つ目の山までは予測できていたのですが・・・この場合も、外挿してはいけないことが良く分かる例となりました。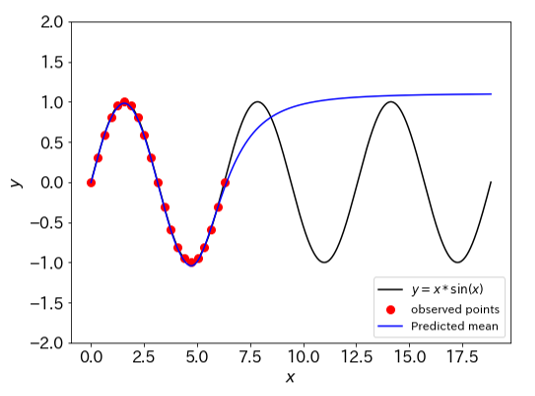

f:id:Dajiro:20200421221014p:plain — ニューラルネットワーク(隠れ層3層, ノード数50, 活性化関数tanh)による外挿。

サポートベクター回帰

続いてサポートベクター回帰です。scikitlearnのデフォルトパラメータのうち、イプシロンチューブの幅を0.01に小さくし過学習するようにしました。どのような結果になるか大体わかるようになってきましたね。学習自体はうまく行えているようですが、そこから少しでもずれると、アウトです。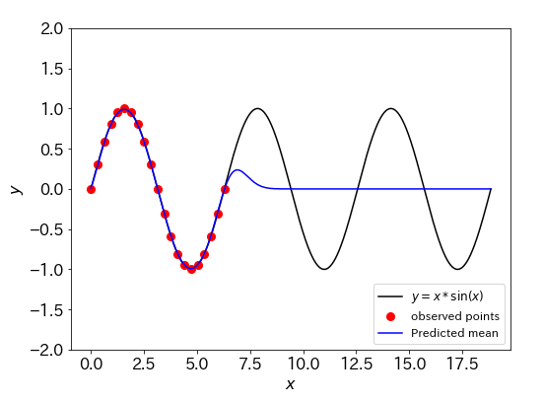

f:id:Dajiro:20200421221043p:plain — SVRによる学習と外挿。

ランダムフォレスト

機械学習３兄弟の３男（？）、ランダムフォレストです。木の深さには制限を設けていません。決定木に基づいた結果らしく、学習データにはカクカク合わせにいっていて面白いですね。いかにもランダムフォレストな特徴だと思います。そして学習データから外れた途端、１直線に伸びていきます、永遠に（？）。この場合もやはり、外挿領域を予測するのは不可能なようです。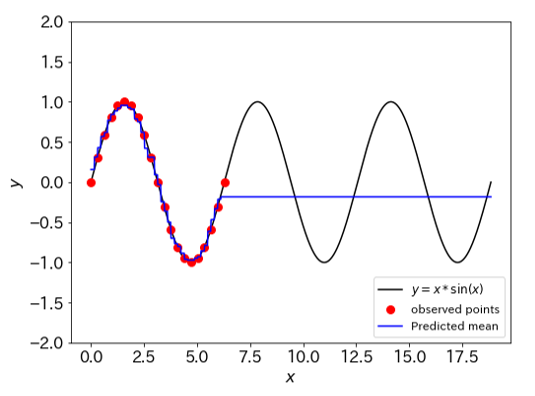

f:id:Dajiro:20200421221756p:plain — カクカク適合ランダムフォレスト、そして永遠にはるか彼方へ。

まとめ

ここで用いたモデルはすべて、学習データに対して非常にうまく内挿できることが既知の事実としてありますが、特にGRPに関してはデータの特徴に応じたカーネルを設計することで外挿にもある程度適用できることが示唆されました。一方で、RBFカーネルを用いた場合のGRPや、NN、RF、SVFの例から明らかなように外挿する場合には十分な注意を払うべし、ということもまたはっきりと分かりました。今回は１入力１出力モデルでしたが、より複数の入力チャネルを持つ場合にも同様のことが言えるはずです。このことから、予測を行う場合には