スコアベース拡散モデルの概要

　こんにちは。前回に引き続き、拡散モデルに関する話題を取り上げます。拡散モデルとはGoogleのImagen等に活用されている話題の生成モデルであり、一部のタスクでは最も研究が進んでいる生成モデルGAN（敵対的生成ネットワーク）の最高性能を上回ることが報告されています。拡散モデルにはスコアベースモデル、拡散確率モデルなど幾つかのタイプがありますが、今回はスコアベースモデルについて解説を行います[1,2,3,4]。

　以下は、スコアベースモデルによる画像生成の実例です。人間の目にはフェイクであることが分からないほどの精度で、画像が生成できています。

エネルギーベースモデルの復習
スコアベースモデルの概要
スコアマッチング
スコアベースモデルの課題
多段階のノイズ付加
更なる改良
おわりに
出典

エネルギーベースモデルの復習

　スコアベースモデルの解説の前に、その基礎となるエネルギーベースモデル（EBM）の考え方を復習します。EBMでは任意のパラメータを持った関数 $E_{\theta}$ について、以下の式で確率密度関数を構成しました。

$p_{\theta}(\boldsymbol{x}) = \frac{\textrm{exp}(-E_{\theta}(\boldsymbol{x}))}{Z_{\theta}}$ ここで、連続値の場合は $Z_{\theta} = \int_{x} \textrm{exp}(-E_{\theta}(\boldsymbol{x}))d\boldsymbol{x}$

$p_{\theta}(\boldsymbol{x})$ は任意のデータ $\boldsymbol{x}$ に対して常に > 0であり、積分（又は総和）すると1になることから確率密度としての要件を満たします。EBMでは対数尤度を最大化するためにパラメータに関する勾配を計算しました。

$\nabla_{\theta}\textrm{log}p_{\theta}(\boldsymbol{x}) = -\nabla_{\theta}E_{\theta}(x_{train}) - \nabla_{\theta}\textrm{log}Z_{\theta}$

ここで問題となるのが、正規化定数 $Z_{\theta}$ の計算です。EBMではマルコフ連鎖モンテカルロ法（MCMC）とcontrastive divergence（CD）を用いることで問題を解決しましたが、MCMCは収束までの時間が遅く、またCDはモデルからデータをサンプリングする必要があり計算コストが重いという問題があります。これらの問題を解決するための手段が、スコアベースモデルです。

EBMの詳細は過去記事をご覧ください。
dajiro.com

スコアベースモデルの概要

　EBMでは $p_{\theta}(\boldsymbol{x})$ の $\theta$ に関する勾配を計算しましたが、スコアベースモデルではデータ $\boldsymbol{x}$ に関する勾配

$\nabla_{x}\textrm{log}p_{\theta}(\boldsymbol{x})$

を解析対象とします。これをスコア関数と呼び $s_{\theta}(\boldsymbol{x})$ と表します。正規化定数 $Z_{\theta}$ は確率変数に依存しませんから、

$s_{\theta}(\boldsymbol{x}) = -\nabla_{x}E_{\theta}(\boldsymbol{x})$

となり正規化定数に依存せずに表現することができます。
　スコアベースモデルでは、モデルのスコア関数と真のデータ分布の勾配のフィッシャー距離を最小化することで学習が行われます。
$\frac{1}{2}\mathbb{E}_{\boldsymbol{x} \sim p(\boldsymbol{x})}[|| \nabla_{x}q(\boldsymbol{x}) - s_{\theta}(\boldsymbol{x})||_{2}^{2}$ ]

しかし真のデータ分布の勾配 $\nabla_{x}p(\boldsymbol{x})$ の計算が難しそうです。ここでスコアマッチングと呼ばれる手法を用いることで、直接データ分布の勾配を計算しなくてもフィッシャー距離を最小化することができます。

スコアマッチング

　上で定義したフィッシャー距離を計算するために、 $\textrm{Hyv}\ddot{a}\textrm{rinen}$ [5]は部分積分を用いて真のデータ分布の勾配への依存性を消去し、以下の式と等価であることを証明しています。

$\mathbb{E}_{\boldsymbol{x} \sim p(\boldsymbol{x})}[\frac{1}{2}||s_{\theta}(\boldsymbol{x})||_{2}^{2} + \textrm{tr}\nabla_{\boldsymbol{x}} s_{\theta}(\boldsymbol{x})$ ]

第二項はスコア $s_{\theta}(\boldsymbol{x})$ のヤコビアンのトレース計算を表しています。この式はモデルのスコアのみを含んでいることから、目的関数を計算することができそうです。一方で問題点もあり、ヤコビアンの計算はデータの次元Dに対して $O(D)$ のオーダーで計算量が増加するため、データのサイズに対してスケールさせることが出来ません。

そこで、この問題を克服するために考案されたのがデノイジングスコアマッチングとスライスドスコアマッチングです[6, 7]。

デノイジングスコアマッチング

　Vincent[6]はクリーンなデータ $\boldsymbol{x}$ とノイズ付きデータ $\tilde{\boldsymbol{x}}$ に対して目的関数を以下のように定義しました。

$\frac{1}{2}\mathbb{E}_{\tilde{\boldsymbol{x}} \sim p_{data}}[||s_{\theta}(\tilde{\boldsymbol{x}}) - \nabla_{\tilde{\boldsymbol{x}}}\textrm{log}q(\tilde{\boldsymbol{x}})||^{2}_{2}$ ]
$= \frac{1}{2}\mathbb{E}_{\boldsymbol{x} \sim p_{data}(\boldsymbol{x}), \tilde{\boldsymbol{x}} \sim q(\tilde{\boldsymbol{x}}|\boldsymbol{x})}[||s_{\theta}(\tilde{\boldsymbol{x}}) - \nabla_{\tilde{\boldsymbol{x}}}\textrm{log}q(\tilde{\boldsymbol{x}}|\boldsymbol{x})||^{2}_{2}$ ]

これにより、モデルから出力されるノイズデータは、ノイズ付きの真のデータに近づこうとします。真のデータに関する第二項の計算は難しそうですが、ここでカーネルトリックを用い、ガウスカーネルを用いて以下のように表現することにします。

$\nabla_{\tilde{\boldsymbol{x}}}\textrm{log}q(\tilde{\boldsymbol{x}}|\boldsymbol{x}) = -\frac{\tilde{\boldsymbol{x}} - \boldsymbol{x}}{\sigma^{2}}$

データがn個あるとすると、目的関数の期待値の計算は最終的に以下のように書き下すことができます。

$\frac{1}{2n}\sum_{i=1}^{n}[||s_{\theta}(\tilde{\boldsymbol{x}}) + \frac{\tilde{\boldsymbol{x}} - \boldsymbol{x}}{\sigma^{2}}||$ ]

スコア関数のヤコビアン計算を消去することが出来ました。これで高次元データにもスケールするスコアマッチングが可能となります。

スライスドスコアマッチング

　高次元空間における勾配の比較をより単純な問題に落とし込むために、Songらは勾配ベクトルを1方向を向いたランダムベクトルに射影することを考えました[7]。

このとき、フィッシャー距離は以下のようにベクトルの積を用いて書くことができます。さらに部分積分を用いて $p_{data}$ への依存性を消去することも可能です。

$\frac{1}{2}\mathbb{E}_{v \sim p_{v}}\mathbb{E}_{\boldsymbol{x} \sim p_{data}}[(\boldsymbol{v}^{T}\nabla_{\boldsymbol{x}} \textrm{log}p_{data}(\boldsymbol{x}) - \boldsymbol{v}^{T}s_{\theta}(\boldsymbol{x}))^{2}$ ]
$= \mathbb{E}_{v \sim p_{v}}\mathbb{E}_{\boldsymbol{x} \sim p_{data}}[\boldsymbol{v}^{T}\nabla_{\boldsymbol{x}}s_{\theta}(\boldsymbol{x})\boldsymbol{v} + \frac{1}{2}(\boldsymbol{v}^{T}s_{\theta}(\boldsymbol{x}))^{2}$ ]

ここで注目すべきは、スコア関数のヤコビアン計算が、ベクトルの内積に対するヤコビアン計算に置き換えられることです。

$\boldsymbol{v}^{T}\nabla_{\boldsymbol{x}}s_{\theta}(\boldsymbol{x})\boldsymbol{v} = \boldsymbol{v}^{T}\nabla_{\boldsymbol{x}}(\boldsymbol{v}^{T}s_{\theta}(\boldsymbol{x}))$ （上式の第一項の変換）

これによりスコア関数ネットワークの出力ノードを１つに集約でき、自動微分を一回実行するだけで、ランダムベクトルに射影したときのデータに対する勾配を計算できるようになります。一方で従来型のスコアマッチングでは、出力ノードの個数はデータ次元数Dだけ存在していたため、D回の自動微分が必要でした。ランダムベクトルの個数MがDより大幅に小さいとすると、スライスドスコアマッチングは大幅に計算量を縮減できるスケーラブルな方法と言えます。

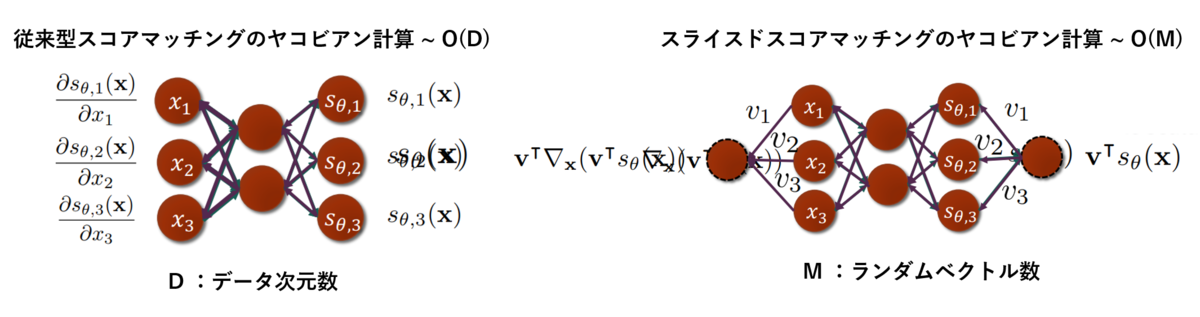
従来法とスライスドスコアマッチングの誤差逆伝搬にかかる計算量比較（出典[8]に加筆）

サンプリング

　真のデータ分布の勾配を近似することが出来たら、それを用いてデータをサンプリングします。エネルギーベースモデルに関する記事でも言及したように、ランジェバン動力学を用いたサンプリングを行います。初期サンプルは何らかの事前分布から生成し、以下の式に基づいて繰り返し更新することで最良のデータを生成します。

$\boldsymbol{x}_{i+1} \leftarrow \boldsymbol{x}_{i} + \epsilon\nabla_{ \boldsymbol{x}}\textrm{log}q( \boldsymbol{x}) + \sqrt{2\epsilon} \boldsymbol{z}_{i}, i = 0, 1, \cdots, K$

ここで $\boldsymbol{z}$ はガウス分布から生成されるノイズです。 $\epsilon$ を無限小に、 $K$ を無限大にもっていくことで解は収束し、最も妥当なサンプルが生成されると考えられます。また学習によって $\textrm{log}q( \boldsymbol{x})$ は $s_{\theta}$ によって近似されており、これを代入することでサンプルが得られます。

　これまで結果をまとめたのが以下の図です。まずは真のデータ分布があり、モデルのスコア関数がこの勾配を近似するようにスコアマッチングを用いて学習を行います。得られた学習済みスコア関数を利用してデータをランジェバン動力学によってサンプリングすることで元のデータを模倣した新しいサンプルが生成されます。

スコアベースモデルの課題

　このように定義したスコアベースモデルには、ある問題があります。それを理解するために、多様体仮説を考えます。多様体仮説とは、実世界のデータは高次元空間に埋め込まれた低次元多様体に集中している、ということを経験的に主張したものです。スコアベースモデルではデータに関する勾配は高次元空間全域で計算しているため、データが少ない領域ではスコアの推定が困難になります。スコアが計算できなければ、ランジェバンダイナミクスではデータの低密度領域を探索することができません。

多段階のノイズ付加

　多様体仮説に基づく問題を回避するために、元のデータにノイズを与える、というアイデアが用いられました。データに完全にランダムなノイズを与えることで、データは低次元多様体に拘束されることなく高次元空間全域に存在するとみなすことができます。ノイズは段階的に付与され、最終的にはデータは完全なノイズとなります。逆に、ノイズを段階的に除去する（アニールする）ことで、データ分布からのサンプリングを行うのがスコアベース拡散モデルの中心的な考え方です。ノイズを段階的に付与する過程は、以下の図のように理解できます。

ガウシアンノイズを付加したときの真のデータ分布は以下のように書くことができます[9]。

$q_{\sigma_{i}}(x) = \int q(y)N(x;y, \sigma_{i}^{2}I)\textrm{d}y$

このノイズ付与分布に対する勾配 $\nabla_{x}\textrm{log}q_{\sigma_{i}}$ を、スコア関数 $s_{\theta}(x, i)$ で推定します。文献[3]ではこのスコア関数をNoise Conditional Score Network(NCSN)と呼んでいます。全部でL段階のノイズが付与されるとしたとき、NCSNを訓練するための損失関数は以下の式で定義されます。

$\sum_{i=1}^{L}\lambda(i)\mathbb{E}_{q_{\sigma_{i}}(x)}[|| \nabla_{x}\textrm{log}q_{\sigma_{i}}(x) - s_{\theta}(x, i)||^{2}_{2}$ ]

と書けます。ここで $\lambda(i)$ はウェイトです。上記で言及したスコアマッチングを用いて上式を計算可能な形へ変換し、学習を行います。

サンプリングは、一様分布などの事前分布から生成したデータを出発点としてannealed Langevin dynamicsを用いて行います。L段階のノイズレベルごとに、異なるステップ幅を用いてT回のランジェバンMCMCを実行しサンプルを生成します。得られたサンプルを出発点として、ステップ幅を変えながら再度サンプルを生成します。これをL回繰り返すことで、最終的なサンプルを生成します。完全にランダムなデータから、サンプルが実際に生成される過程が以下の図です。リアルな画像が生成されている様子が見て取れます。

更なる改良

　以上がスコアベースモデルの概要となります。生成画像の更なる高精度化のために、多くのテクニックが既に開発されています。ここでは詳細は触れませんが、そのうちいくつかをピックアップします。上記の説明ではノイズの付加を段階的に行っていましたが、Songらはこれを連続的な過程と見做すために確率微分方程式として定義しています[4]。ノイズからデータを生成するための確率微分方程式のソルバーとしてEuler-Maruyama法を用い、さらにPredictor-Corecctor機構を導入し、ステップごとに予測されるサンプルの品質をスコア関数を用いて補正する、といったテクニックを用いることで、素朴なスコアベースモデルから大幅な高精度化を実現しています。
　また、スコアベースモデルと異なるタイプの拡散モデルとして、拡散確率モデルが知られています。そちらのアプローチは以下のブログが詳しいです[10]。数式が多く読み進めるのが大変ですが、一言で述べるならノイズの除去方法をニューラルネットワークで学習しています。Kerasによる画像生成例も公開されています[11]。

おわりに

　以上、スコアベースモデルの概要について説明しました。様々なテクニックが盛りだくさんで学習コストが非常に高く、GANやVAEより難しく感じました。最近は有志による英語ブログ記事が増えており、youtubeでの日本語解説も行われているので徐々にハードルは下がっていくでしょう。拡散モデルのスピーチ生成や分子生成等の応用例についても、学習を続けていきたいと思います。