【エネルギーベースモデル】EBMの仕組みと拡散モデルとのつながり

　こんにちは。今回は、深層学習における生成モデルの１つであるエネルギーベースモデル（EBM）について解説します。EBMは深層学習のブレイク以前からある伝統的な技術ですが、最近Googleが発表したImagen等の超高精度生成モデルで使われる拡散モデルと深い関わりがあります。拡散モデルは主にスコアベースモデルと確率拡散モデルの2通りの流儀があり、両者を統合したモデルはまだ確立していない模様です[1, 2]。今回取り上げるEBMは前者のスコアベースモデルを理解する上で必須の技術です。そのため本記事と次回の投稿で、それぞれEBMとスコアベースモデルの解説を行います。

　EBMに関する日本語記事は、意外と出てきません。本記事の執筆にあたりアムステルダム大[3]、スタンフォード大[4]、ニューヨーク大[5]の公開されている講義資料を参考にしました。これらの海外有名大学が講義で扱っていることからも、その重要性を伺い知ることができます。

各種生成モデルの振り返り
エネルギーベースモデルの概要
学習方法
サンプリング
訓練アルゴリズム
学習結果
出典

各種生成モデルの振り返り

　生成モデルでは、あるデータが何らかの高次元確率分布からサンプリングされたものであると仮定し、その確率分布を近似的に求めることが多いです。確率分布の求め方として、変分オートエンコーダ(VAE)では確率分布そのものではなく変分下限（Evidence Lower BOund, ELBO）を押し上げることで確率分布のもっともらしさを最適化します。正規化フローは確率分布そのものを逆変換可能な関数で直接近似しています。一方、敵対的生成ネットワーク（GAN）は異端児的な存在であり、確率分布を直接最適化せずに識別器と生成器を敵対的に訓練することで乱数からデータを発生させることが出来ます。

エネルギーベースモデルの概要

　今回のターゲットであるEBMも確率分布を何らかの形で最適化するという戦略は、多くの生成モデルと共通しています。EBMでは、学習に使うデータ（画像など）を入力とし、スカラー値を出力とするニューラルネットワーク $E_{\theta}(\boldsymbol{x})$ に対して、以下の形で確率分布 $q_{\theta}(\boldsymbol{x})$ を定義します。

$q_{\theta}(\boldsymbol{x}) = \frac{\textrm{exp}(-E_{\theta}(\boldsymbol{x}))}{Z_{\theta}}$ ここで、連続値の場合は $Z_{\theta} = \int_{x} \textrm{exp}(-E_{\theta}(\boldsymbol{x}))d\boldsymbol{x}$

ここで、 $Z_{\theta}$ は分配関数と呼ばれます。分子に含まれる $E_{\theta}$ はエネルギーと呼ばれ、エネルギーを小さくする $\boldsymbol{x}$ で確率分布がより高くなるように学習が進められます。

これは確率分布ですから、以下の条件を満たすか確認しておきましょう。
$q_{\theta}(\boldsymbol{x}) \geq 0$
$\int_\boldsymbol{x} q_{\theta}(\boldsymbol{x})d\boldsymbol{x} = 1$

$q_{\theta}(\boldsymbol{x})$ の定義式の分子は指数関数のため常にゼロ以上の数値となりますし、分母は分子を確率変数で積分（離散値であれば和）していますから $q_{\theta}(\boldsymbol{x})$ の積分が1になることも容易に確かめることが出来ます。以上から、このように定義した $q_{\theta}(\boldsymbol{x})$ がデータ分布を表す確率分布として使えることが分かります。
　
　確率分布をこのように定義するメリットとして、 $E_{\theta}$ にはどのような関数を置いてもよいため優れた柔軟性があります。一方でデメリットとなるのは $Z_{\theta}$ の計算の難しさです。これを求めるには高次元変数 $\boldsymbol{x}$ に関する積分が必要ですが数値計算のコストが高く、解析的に書き下すこともできません。しかし幸いなことに、以下に示すようにContrastive divergenceと呼ばれる手法により直接 $Z_{\theta}$ を計算しなくても $q_{\theta}(\boldsymbol{x})$ を最適化することができます。

学習方法

　EBMの学習において、私たちのゴールは $q_{\theta}(\boldsymbol{x}) = \frac{\textrm{exp}(-E_{\theta}(\boldsymbol{x}))}{Z_{\theta}}$ を最大化するためにパラメータ $\theta$ を最適化することです。そのため対数尤度の勾配（に負号をかけたもの）を以下のように計算します[4]。

$\nabla_{\theta}E_{\theta}(x_{train}) + \nabla_{\theta}\textrm{log}Z_{\theta}$
$= \nabla_{\theta}E_{\theta}(x_{train}) + \frac{\nabla_{\theta}Z_{\theta}}{Z_{\theta}}$
$= \nabla_{\theta}E_{\theta}(x_{train}) + \frac{1}{Z_{\theta}}\int \nabla_{\theta}\textrm{exp}(-E_{\theta}(x))dx$
$= \nabla_{\theta}E_{\theta}(x_{train}) - \int \frac{\textrm{exp}(-E_{\theta}(x))}{Z_{\theta}}\nabla_{\theta}E_{\theta}(x)dx$
$= \nabla_{\theta}E_{\theta}(x_{train}) - \mathbb{E}_{sample}[\nabla_{\theta}E_{\theta}(x_{sample})$ ]
$\approx \nabla_{\theta}E_{\theta}(x_{train}) - \nabla_{\theta}E_{\theta}(x_{sample})$

つまり、エネルギー $E_{\theta}$ について訓練データ $x_{train}$ , モデルからサンプリングされたデータ $x_{sample}$ を入力としたときの $\theta$ に関する勾配をtrainは大きく、sampleは小さくすることで学習が実現するという直感的にも理解しやすい形式に落とし込むことが出来ました。これをContrastive divergenceと呼びます。これは図で書くと以下の通りで、学習によってサンプルデータに対する数値を引き下げ、逆に訓練データに対する数値を引き上げるように最適化が行われるイメージです。図の $f_{\theta}$ は $-E_{\theta}$ に対応しており、 $q_{\theta}(\boldsymbol{x}_{train})$ の分子が大きく、分母が小さくなることが私たちの望む結果です。

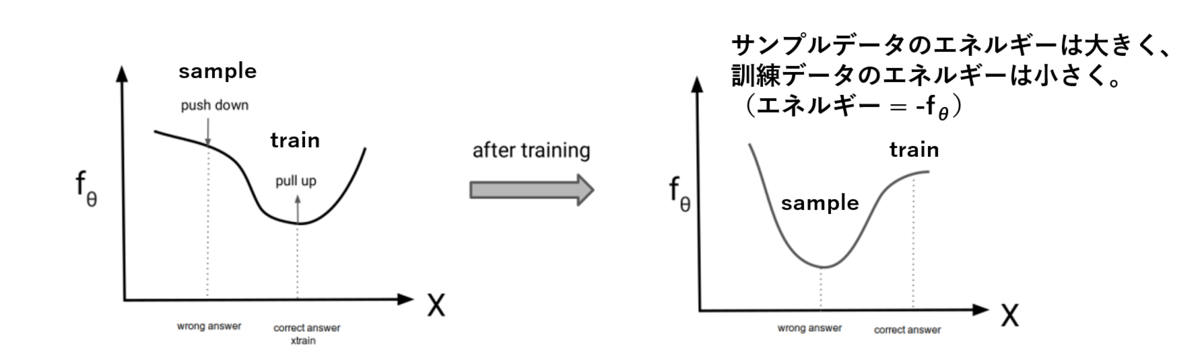
このように目的関数が得られましたが、次の問題はどうやってモデルからデータ $x_{sample}$ をサンプリングするか、ということです。

サンプリング

　分配関数 $Z_{\theta}$ を直接計算することなしにサンプリングすることを考えます。これはマルコフ連鎖モンテカルロ法（MCMC）で実現できますが、収束に非常に時間がかかることが知られています。そこでMCMCにランジュバン動力学の考え方を適用することにより、効率的にサンプリングできるようにします。サンプリングアルゴリズムは以下の通りです。

1. 何らかの事前分布（ガウス分布、一様分布など）からサンプル $\boldsymbol{x}^{0}$ を生成。
2. $\boldsymbol{x}^{t}$ と確率分布の勾配 $\nabla_{x}\textrm{log}q_{\theta}(\boldsymbol{x})$ , 及びノイズ $\omega$ を用いて以下の式により $\boldsymbol{x}$ を更新：
　 $\boldsymbol{x}^{t+1} = \boldsymbol{x}^{t} + \eta\nabla_{x}\textrm{log}p_{\theta}(\boldsymbol{x}) + \omega$
　ここにt = 0, 1, 2, ... T-1、ノイズ $\omega$ はガウス分布から生成されたとする。
3. Kステップ更新により打ち止め、 $\boldsymbol{x}_{sample} = \boldsymbol{x}^{K}$ とする。

ここで、分配関数の $\boldsymbol{x}$ の微分はゼロとなるため、 $\nabla_{x}\textrm{log}q_{\theta}(\boldsymbol{x}) = - \nabla_{x}E_{\theta}(\boldsymbol{x})$ となり、めでたく $\boldsymbol{x}_{sample}$ を $Z_{\theta}$ に依存しない形で求めることができました。ちなみに $\nabla_{x}\textrm{log}q_{\theta}(\boldsymbol{x})$ はスコア関数と呼ばれ、次の投稿で扱うスコアベースモデルで中心的な役割を果たします。

訓練アルゴリズム

　ここで訓練アルゴリズムを整理してみましょう[3]。以下に概要を示します。まず事前分布から初期サンプルを生成し、ランジュバンMCMCによってサンプリングします。それと訓練データをもとにcontrastive divergenceを計算します。ここで、学習を安定化させるために損失関数に正則化項を加えていることに注意です。それらの損失を用いてAdamやSGDといったオプティマイザでパラメータを最適化します。また、サンプリング効率を上げるため、サンプリングバッファを設けるテクニックがあります。これは数バッチ前のサンプルをバッファに蓄え、これをランジェバンMCMCにおける初期値とすることで収束を早めます。とはいえ未知のデータに対するサンプリングも行うべきなので、全体の5%を再度初期化してサンプリングするという処理を施すこともあります。
　こうした学習を行うことで確率分布が訓練データの分布に近いものになるはずです。学習後の分布から生成されるサンプルは、訓練データに類似した特徴を有していることが期待されます。

学習結果

　エネルギーを求めるのに一般的なCNNを用い、出典[3]に基づいて画像を生成した結果がこちら。MCMCのステップ数に応じて、ランダムな初期サンプルからデータがどのように変わるかを示しています。初期は完全にランダムですが、はやくも32ステップでMNIST画像らしさを獲得していることが分かります。その後は極端に大きな変化はないように見えますが、上段と下段のサンプルは最終的に数字の２と0を生成しているように見えます。一方で中段は具体的にどの数字か判別しかねます。

もう少し初期のイタレーションの結果を細かく見てみます。完全なランダムから、数イタレーションのループを回すと実体が浮かび上がってくる様子が見て取れます。

おわりに

　EBMは他の生成モデルと同様に確率密度関数の対数尤度の最大化を目指して学習が行われますが、ノイズから意味のあるデータが徐々に浮かび上がってくる過程が非常に印象的です。EBMで登場した学習プロセスは計算コストが高いため、上述のスコア関数を効率的に真のデータ分布の勾配に近づけるスコアマッチングと呼ばれる手法を使ったスコアベースモデルが盛んに研究されています。次回の投稿では拡散モデルへと進んでいきましょう。