機械学習の分野で最も有名なモデルに畳み込みニューラルネットワーク(CNN)と呼ばれるものがあります。2012年にCNNが画像認識処理において卓越した性能を示したことで科学や生活の在り方は大きく変わりました。この手法は画像(2次元データ)のみならず波形のような1次元データに対しても転用可能です。本記事では、スマートホンのセンサから取得した人の行動波形に関する畳み込みニューラルネットワークのPyTorchによる計算方法を紹介します。またOptunaを用いたハイパーパラメータ探索によってハイパーパラメータの探索やその重要度評価が可能となります。計算手順を追ってみていきましょう!
学習用データ
学習用データには、スマートホンのセンサーから取得した人間の行動データとその時の実際の行動(歩行、階段を上る、階段を下る、座る、起立する、横たわる)に対応したラベルからなる約1万件のデータセットを用いました。また、行動データには加速度計とジャイロセンサから取得した9通りの波形データが含まれています。つまり、9チャネルの1次元データから6通りの行動様式を予測する分類モデルを構築することが、本タスクの目的となります。
UCI Machine Learning Repository: Human Activity Recognition Using Smartphones Data Set

プログラム説明
Jupyter notebook形式のプログラムはGithubで公開しています。実際に動かしてみたい、コードの詳細を確認したい方は以下をご覧ください。
github.com
学習データの読み込み方法は省略しますが、プログラムを実行することで(データサイズ×次元数×チャネル数)=(10299×128×9)のデータが訓練用とテスト用に分けて取得できます。
学習モデルは以下のように定義しました。入力データのサイズ設定を省略するため、pytorch-pfn-extrasのLazyModuleを用いました。また1D畳み込み層のチャネル数、カーネルサイズ、全結合層の出力ノード数を探索対象のハイパーパラメータとして設定しました。画像認識で使う2D畳み込みと異なる部分は、もうここだけです。
GitHub - pfnet/pytorch-pfn-extras: Supplementary components to accelerate research and development in PyTorch
#pytorch-pfn-extrasを使用 import pytorch_pfn_extras as ppe class Net(nn.Module): def __init__(self, channel, kernel, h1, h2): super(Net, self).__init__() self.conv1 = ppe.nn.LazyConv1d(None, channel, kernel) self.pool = nn.MaxPool1d(2, 2) self.conv2 = ppe.nn.LazyConv1d(None, channel, kernel) self.fc1 = ppe.nn.LazyLinear(None, h1) self.fc2 = ppe.nn.LazyLinear(None, h2) self.fc3 = ppe.nn.LazyLinear(None, 6) def forward(self, x): x = self.pool(F.relu(self.conv1(x))) x = self.pool(F.relu(self.conv2(x))) x = x.flatten(start_dim=1) x = F.relu(self.fc1(x)) x = F.relu(self.fc2(x)) x = self.fc3(x) return F.log_softmax(x, dim=1) #モデルにダミーデータを通して省略していたモデルのパラメータを決定する model = Net(channel, kernel, h1, h2) dummy_input, _ = next(iter(train_loader)) model(dummy_input.float())
残りで特筆すべき点はOptunaの実装です。objective関数の中に探索対象のパラメータを設定し学習モデルを実装します。また関数の戻り値には最適化対象のパラメータを設定します。ここでは正答率を最大化したいため、accuacyを戻り値に設定しています。ここでは重要度を評価したいので、ハイパラの探索方法にはランダムサーチを指定します(そうしないとパラメータの探索範囲が偏り、重要度を正しく評価できないため)。また正答率を最大化するため、direction="maximize"を設定する必要があります(デフォルトでは最小化)。
def objective(trial): #学習率、バッチサイズ、チャネル数、カーネル、隠れ層ノード数を探索対象に指定 lr = trial.suggest_float('lr', 1e-5, 1e-2, log=True) batch_size = trial.suggest_int('batch_size', 2, 4096) channel = trial.suggest_int('channel', 2, 128) kernel = trial.suggest_int('kernel', 2, 32) h1 = trial.suggest_int('h1', 2, 128) h2 = trial.suggest_int('h2', 2, 128) """"学習モデルの実装""" return accuracy study = optuna.create_study(sampler=RandomSampler(), direction = "maximize") study.optimize(objective, n_trials=100)
非常にざっくりとした説明ですが、詳細はレポジトリのコードをご覧ください!
結果の分析
さて、パラメータ探索の結果を見てみましょう。以下のコードで各ステップ(計100ステップ)のパラメータの組み合わせとそのときの正答率が得られます。またget_param_importancesで正答率に影響したパラメータの重要度を評価できます。デフォルトではランダムフォレストによって重要度を評価する手法が内部で動いているようです。
#結果をデータフレーム形式で取得 df = study.trials_dataframe() #重要度を辞書形式(OrderedDict)で取得 imp = optuna.importance.get_param_importances(study)

重要度を見ると、チャネル数>バッチサイズ>隠れ総数2>学習率>隠れ総数1>カーネルサイズの順で影響度が大きいことが分かります。学習モデルの構造に依存することも多そうですが、チャネル数の設定には敏感になった方が良さそうです。とはいえ、探索ステップ数をさらに増やしたとき、同じ序列が保たれているのかは不明です。1つの参考情報として留めておくのがベターなように思われます。

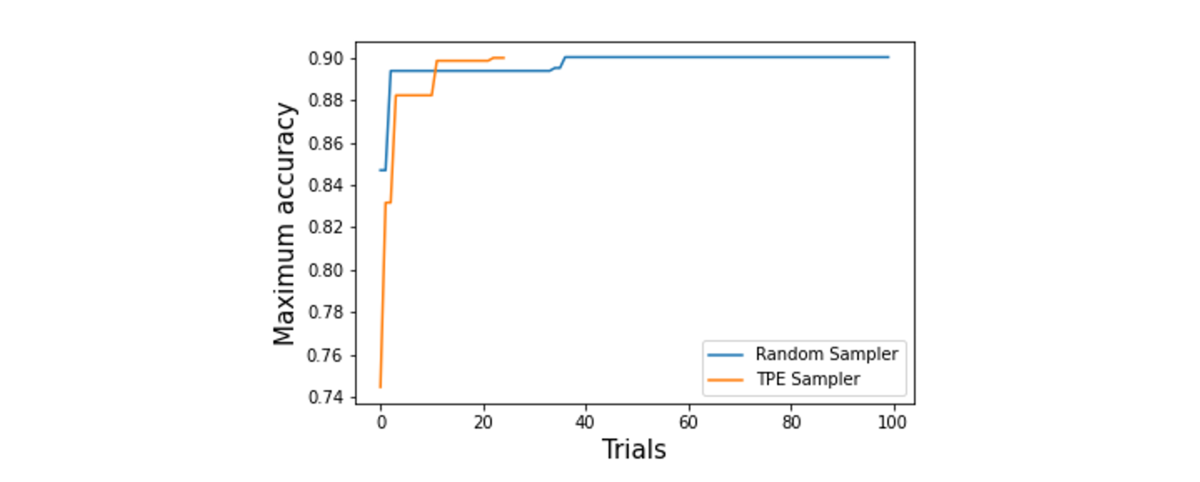
ついでに、Random SamplerとTPE(Tree-structured Parzen Estimator)を用いたハイパラ探索の効率を比較してみたいと思います。分かりづらいかもしれませんが、横軸が探索ステップ数で右に行くほど探索が進んでいます。縦軸はそのステップ終了時点での正答率の最大値で右上に伸びていくのが正しい挙動です。最終的に到達した最大正答率は2つのサンプラーでほぼ同等ですが(~0.90)、やはりランダムサーチの方が効率が悪いことが見て取れます。TPEでは25ステップで高い精度が得られています。
終わりに
1DCNNを初めて使いましたが、2DCNNとまったく同じ使用感で動作可能であることが分かりました。またOptunaによるハイパラ探索の結果、今回のタスクに関してはチャネル数やバッチサイズに対して正答率が敏感である可能性が示唆されました。また、元の学習データ提供元が報告しているテストデータに対する予測精度(~89%)と同程度のハイパーパラメータに到達することを確認できました。世の中に波形データは数多く存在し解析する場面も決して少なくありません。1DCNNのほかの解析手法も調査してみたいと思います。