こんばんは。先日、Graph Attention Networksに関する解説記事を書きました。ここではグラフデータを読み込んで、グラフの頂点に割り当てられたラベルを予想するというタスクを解きました。データセットには論文の引用関係を示したCoraデータセットを使いましたが、今日はこのCoraデータセットがどのようなグラフなのかをNetworkXというグラフ計算用のライブラリを使って可視化してみました。
Graph Attention Networksの記事はこちらになります。
dajiro.hatenablog.com
また、本稿執筆には以下の資料を参考にさせて頂きました。

Pythonで学ぶネットワーク分析: ColaboratoryとNetworkXを使った実践入門
- 作者:剛志, 村田
- 発売日: 2019/09/15
- メディア: 単行本
NetworkX
NetworkXは複雑なネットワークの構築、ネットワークの特徴の計算(類似性やつながりの数など)、グラフの描画などを扱えるPythonライブラリです。内部的にはFortranやCで動いており高速計算が可能とのこと。2002年に誕生したライブラリですが、近年グラフニューラルネットワークが注目されていることからNetworkXの存在感も増していく気がしています(本稿はそうなることを予想して、筆者の勉強もかねて執筆しているわけです)。
networkx.github.io
Coraデータセット
すでにGraph Attention Networksの記事内でも書いていますが、繰り返します。Coraデータセットには機械学習系の2708報の論文の引用・被引用関係と論文のラベルの情報が格納されています。このデータセットはcora.citesとcora.contentという2つのファイルから構成されており、cora.contentには
(paper_id) (word_attributes) + (class_label)
というフォーマットで論文のID, word_attribute(その論文の特徴量に相当, 1433次元), ラベルが並んでいます。ここでword_attributeは学習データの全論文の頻出単語として選び出した1433単語について、その論文に含まれていれば1、なければ0を格納したベクトルになります。ラベルは、以下の7つのクラスのいずれかが割り当てられています。
- Case_Based,
- Generic_Algorithms,
- Neural_Networks,
- Probabilistic_Methods,
- Reinforcement_Learning,
- Rule_Learning,
- Theory
このデータの束が2708個入っています。
続いてcora.citesには論文の引用関係が以下のようなフォーマットで格納されています。
(ID of cited paper) (ID of citing paper)
引用された・引用した論文IDです。これは全部で5429個あるので、論文同士のネットワークに計5429個の関係が存在するということを意味しています。
可視化手順
1.Coraデータセットの配列化
NetworkXの機能によって、グラフ構造を表すnumpy形式の行列からNetworkXで扱えるグラフ形式に変換できるメソッドが用意されています。まずは、Coraデータセットのグラフ構造をnumpyの配列に落とし込みましょう。ここでは、Graph Attention Networksで用いられていた実装を参考にしています。
筆者はconda環境で作業しているのでconda install networkxでインストールしたのち、ライブラリをインポートします。
import networkx as nx from networkx.algorithms import community import matplotlib.pyplot as plt import numpy as np import scipy.sparse as sp import pandas as pd
以下のコードでnumpy形式の配列と、頂点に割り当てられるラベルをゲットします。Coraデータセットは2708個のグラフの頂点(論文数)を含んでおり取り出される配列は2708×2708の正方行列です。引用関係がある場合には行列の要素に1が格納されますが、最後に隣接行列の標準化を行っている点に注意してください。私の力不足のためうまく表現できないのですが、これにはつながっている頂点の数に応じて辺の重みを調整する役割があります。つながりが多いほど各辺の重みは小さくなります(例えば友達が沢山いる人は、友達が一人しかいない人よりも友達一人一人の重要度は下がりますよね、という説明で良いのだろうか・・・)。これを入れることで、グラフを可視化したときラベルごとに良く分離してくれたので標準化させました。
隣接行列の標準化については以下の記事を参考にしました。
Interpretation of Symmetric Normalised Graph Adjacency Matrix? - Mathematics Stack Exchange
#次数行列で隣接行列を標準化 def normalize_adj(mx): rowsum = np.array(mx.sum(1)) r_inv_sqrt = np.power(rowsum, -0.5).flatten() r_inv_sqrt[np.isinf(r_inv_sqrt)] = 0. r_mat_inv_sqrt = sp.diags(r_inv_sqrt) return mx.dot(r_mat_inv_sqrt).transpose().dot(r_mat_inv_sqrt) def load_data(path="../pyGAT/data/cora/", dataset="cora"): #論文ID, 特徴量, ラベルの読み込み idx_features_labels = np.genfromtxt("{}{}.content".format(path, dataset), dtype=np.dtype(str)) #ラベルをone-hotベクトルに変換 labels = idx_features_labels[:, -1] classes = set(labels) classes_dict = {c: np.identity(len(classes))[i, :] for i, c in enumerate(classes)} labels = np.array(list(map(classes_dict.get, labels))) # 論文IDを辞書のキー, 順番を辞書の値として保存 idx = np.array(idx_features_labels[:, 0], dtype=np.int32) idx_map = {j: i for i, j in enumerate(idx)} #論文の引用関係を読み込み edges_unordered = np.genfromtxt("{}{}.cites".format(path, dataset)) edges = np.array(list(map(idx_map.get, edges_unordered.flatten()))).reshape(edges_unordered.shape) #隣接行列に変換, メモリ節約のためにscipy.sparseモジュールを活用 adj = sp.coo_matrix((np.ones(edges.shape[0]), (edges[:, 0], edges[:, 1])), shape=(labels.shape[0], labels.shape[0])) # 隣接行列を対称行列に変換 adj = adj + adj.T.multiply(adj.T > adj) - adj.multiply(adj.T > adj) #隣接行列の標準化, 接続しているノードの数に応じてエッジに重みがかかる adj = normalize_adj(adj + sp.eye(adj.shape[0])) adj = np.array(adj.todense()) labels = np.where(labels)[1] return adj, labels
2.行列をNetworkXのグラフ形式に変換
これはめちゃくちゃ簡単です。対称行列の場合、以下の操作でサクッとできます。
G = nx.from_numpy_array(adj)
Gには頂点の名前や辺の情報が格納されており、G.nodes(), G.edges()などで確認できます。更に、各辺に対する重みは G.edges(data=True)で表示できます。試しに表示してみましょう。
print(list(G.edges(data=True))[:10]) [(0, 0, {'weight': 0.16666666666666666}), (0, 8, {'weight': 0.16666666666666666}), (0, 14, {'weight': 0.09128709291752768}), (0, 258, {'weight': 0.11785113019775792}), (0, 435, {'weight': 0.16666666666666666}), (0, 544, {'weight': 0.18257418583505536}), (1, 1, {'weight': 0.5000000000000001}), (1, 344, {'weight': 0.12500000000000003}), (2, 2, {'weight': 0.19999999999999998}), (2, 410, {'weight': 0.18257418583505536})]
3.グラフの可視化
それでは可視化してみましょう。といってもグラフの可視化は決して自明な話ではなくて、満たすべき制約(隣接する頂点同士は近くに配置する、頂点は重ならないようにする、など)を考慮した上で可視化する必要があります。例えば以下の方法があるようです。
- バネ配置
- スペクトラル配置
- 円周配置
- ランダム配置
多くの場合バネ配置が用いられるそうで、これは頂点間を結ぶ辺をバネに見立て、制約を満たすように各頂点に引力・斥力を与えることでグラフを配置します。このようにして頂点を移動させ、最終的に安定した場所がグラフの可視化構造になります(間違っていたらすみませんが、辺の重みはバネ定数に相当?)。以下の場合でもこのバネ配置モデルに基づいた作図を行っています。下のコードでは、nx.spring_layoutでバネ配置に基づいた座標を各頂点に与え、nx.draw_networkx_nodes、nx.draw_networkx_edgesでそれぞ頂点と辺をプロットしています。
また、各論文には7通りのカテゴリが割り当てられていると上で述べましたが、カテゴリごとに色分けして表示します。
node_color = [] node1, node2, node3, node4, node5, node6, node7 = [], [], [], [], [], [], [] colorlist = ['#e41a1c', '#377eb8', '#4daf4a', '#984ea3', '#ff7f00', '#ffff33', '#a65628'] for n, i in enumerate(labels): if i == 0: node_color.append(colorlist[0]) node1.append(n) elif i == 1: node_color.append(colorlist[1]) node2.append(n) elif i == 2: node_color.append(colorlist[2]) node3.append(n) elif i == 3: node_color.append(colorlist[3]) node4.append(n) elif i == 4: node_color.append(colorlist[4]) node5.append(n) elif i == 5: node_color.append(colorlist[5]) node6.append(n) elif i == 6: node_color.append(colorlist[6]) node7.append(n) #バネ配置を用いた場合の各頂点の座標を獲得 pos = nx.spring_layout(G, seed = 42) plt.figure(figsize = (10, 10)) nodelist = [node1, node2, node3, node4, node5, node6, node7] labellist = ['Theory', 'Reinforcement_Learning', 'Neural_Networks', 'Case_Based', 'Probabilistic_Methods', 'Rule_Learning', 'Genetic_Algorithms'] for num, i in enumerate(zip(nodelist, labellist)): n, l = i[0], i[1] #ラベルごとに頂点をプロット nx.draw_networkx_nodes(G, pos, nodelist=n, node_size = 5, node_color = colorlist[num], label=l) #エッジをまとめてプロット nx.draw_networkx_edges(G, pos, width = 0.25) plt.legend(bbox_to_anchor=(1, 1), loc='upper left') plt.savefig("cora.png", dpi = 150, bbox_inches="tight")
この結果がこちらになります。図中央では各頂点が複雑なネットワークを形成しており、それを取り囲むように関係性の薄い頂点が点在しています。また、同じカテゴリの論文(頂点)が割と近い領域に位置しているように見えませんか?このことから論文間の関係性をうまく学習すれば、その論文のカテゴリは予測できそうだという期待が湧くわけですね。やはり可視化は大事ですね。
中心性の分析
せっかくなので簡単な解析も行ってみましょう。ネットワーク分析において中心性という概念はかなり基本的なようです。中心性には様々な定義があり、他の多くの頂点とつながっている頂点を中心としたり(SNSのインフルエンサーのようなもの)、他の頂点への平均到達距離が最短であるもの(都市計画における重要拠点の配置)などがあります。主な中心性としては以下のものがあるようです。
- 次数中心性(もっともつながっている頂点)
- 近接中心性(ほかの頂点との平均距離が短い)
- 固有ベクトル中心性(周囲の頂点の中心性も考慮)
- 媒介中心性(2頂点を結ぶ経路上にしばしば現れる点を中心的とする)
4つとも可視化してみましょう。以下のコードで図が得られます。中心性の値ごとにカラーマップで分けて示しています。また中心性が高いものほど頂点を表すマーカーのサイズも大きくしてあります。
plt.figure(figsize = (12, 12)) #ここで中心性の種類を選択 #次数中心性ならnx.degree_centrarity #固有ベクトル中心性ならnx.eigenvector_centrality #媒介中心性ならnx.betweenness_centrality #近接中心性ならnx.closeness_centralityとする cent = nx.degree_centrality(G) node_size = list(map(lambda x:x*500, nx.degree_centrality(G).values())) nodes = nx.draw_networkx_nodes(G, pos, node_size = node_size, cmap=plt.cm.plasma, node_color=list(cent.values()), nodelist=list(cent.keys())) edges = nx.draw_networkx_edges(G, pos, width = 0.25) plt.colorbar(nodes) plt.show()
次数中心性
辺がたくさんつながった場所が次数中心性の高い場所となるわけですが、確かにその傾向は見て取れますね。特に黄色の点で塗られた頂点、なにかブレイクスルーでも起こしたんですかね笑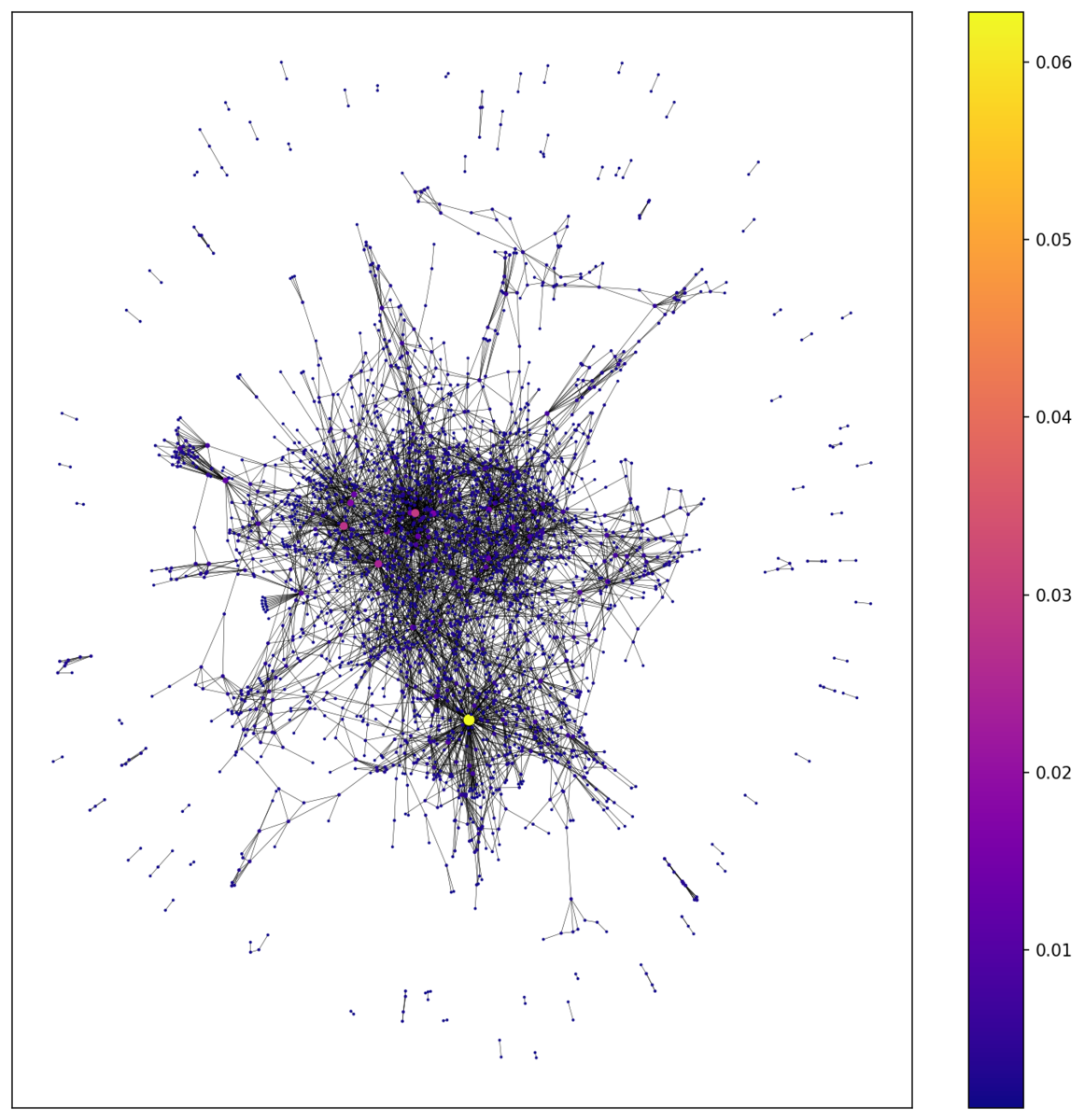
固有ベクトル中心性
まわりの頂点の中心性も考慮する固有ベクトル中心性がこちら。黄色の頂点を取り囲む頂点の中心性も高くなっているのが分かりますね。この場合イノベーティブな論文を引用しただけでその論文の中心性もあがる?とするとあまり適切ではない気もします。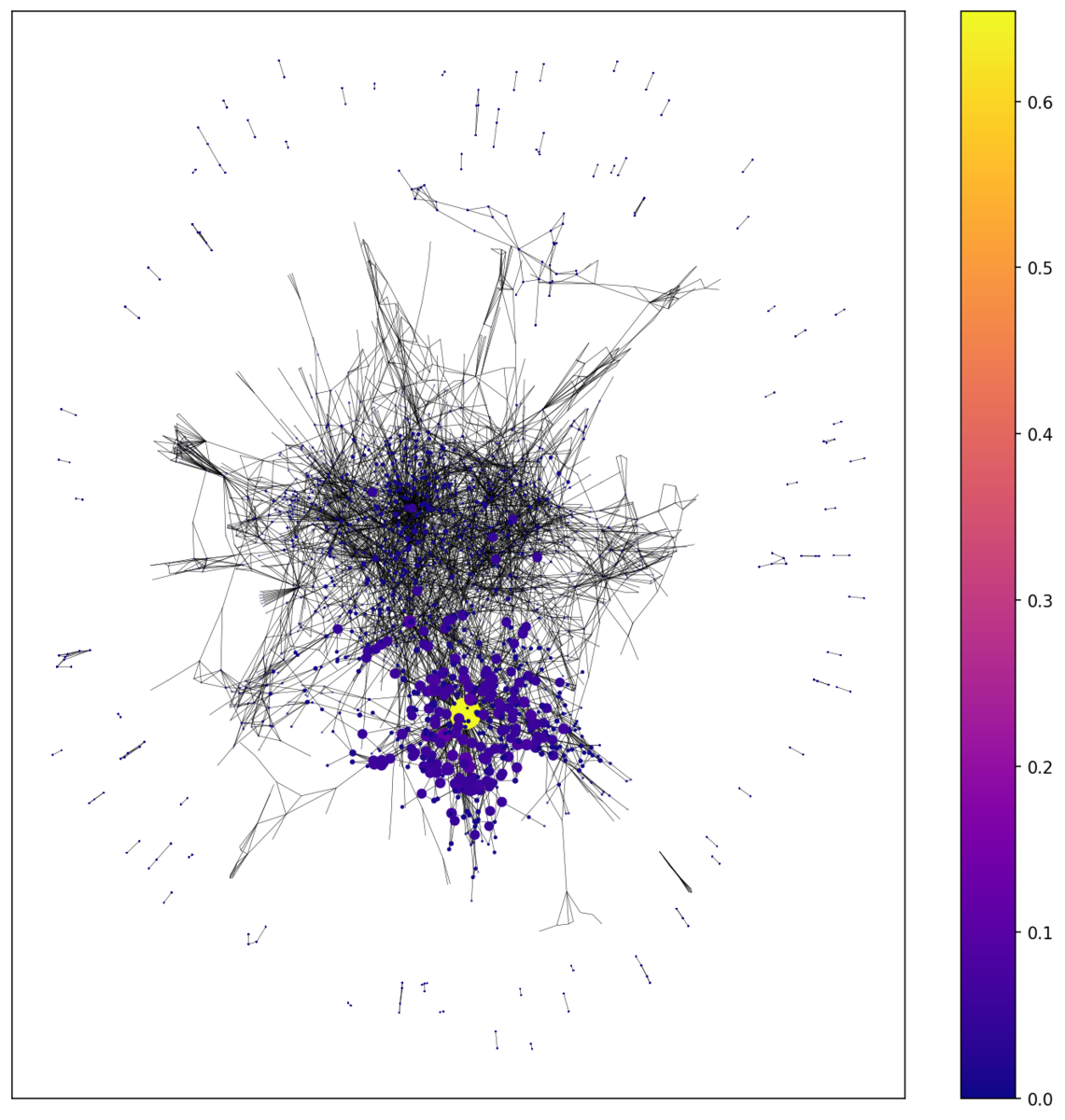
媒介中心性
二頂点を結ぶ経路に頻繁に表れる頂点が、高い中心性を持ちます。次数中心性と似た傾向ですが、新しい研究を生む研究と解釈できるでしょうか?重要論文の絞りこみには使えそうですね。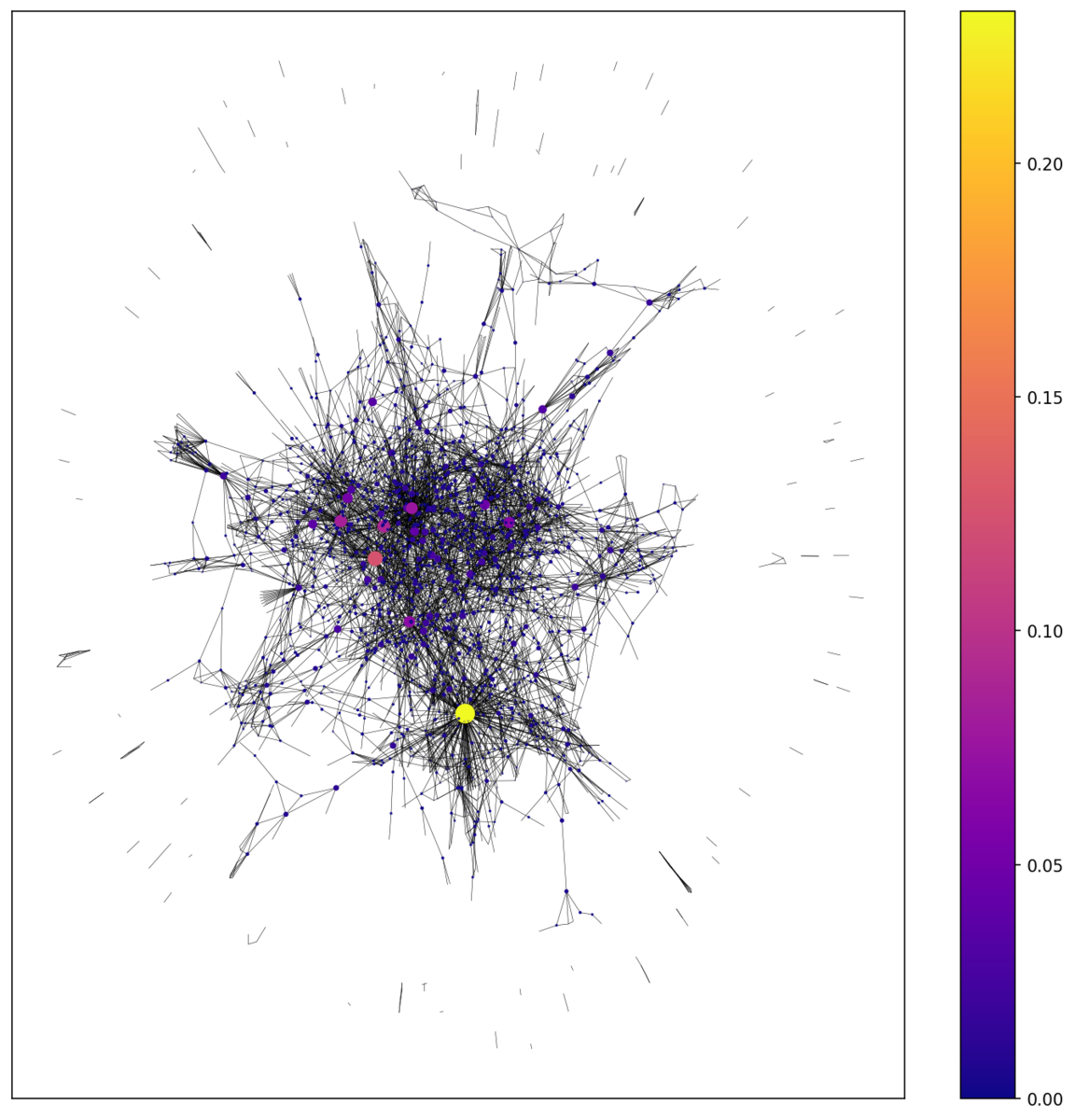
近接中心性
他の頂点との距離が近い頂点が高い中心性を持ちます。Coraデータセットでは多くの頂点が中心付近に密集しているため、多くの頂点の中心性が高くなってしまいめちゃくちゃな図になりました。見事に落ちをつけてくれましたねw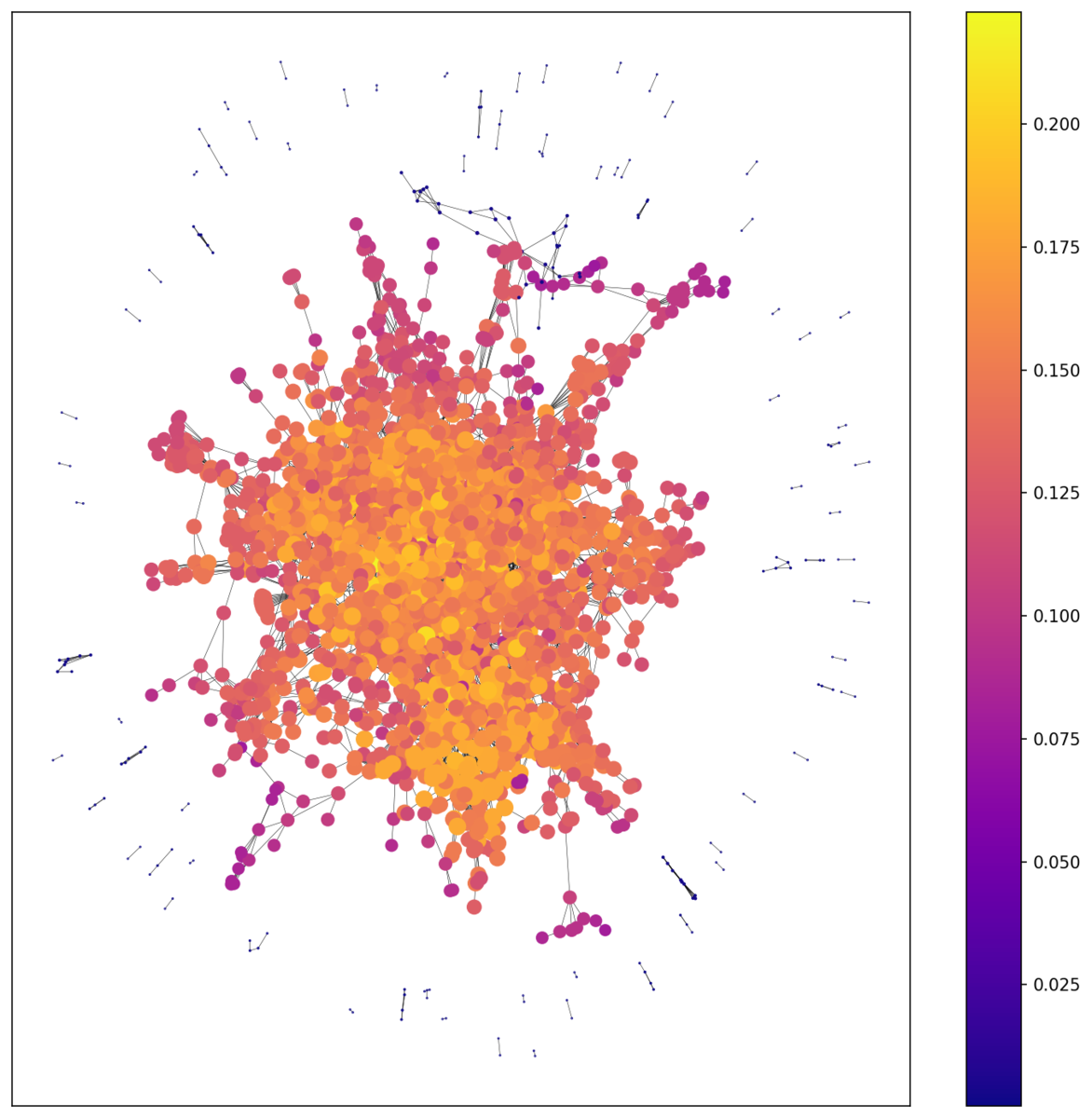
おわりに
グラフデータの可視化は初めて行いました。Coraデータセットのような複雑なネットワークの場合、可視化しないことにはどのようなデータなのかピンとこないためNetworkXによる可視化は非常に有用であると感じました。またニューラルネットワークにもっていかずとも、中心性解析などでグラフの性質を知る手段は豊富にあることも確認できたのが良かったです。他にはコミュニティ検出などの話題も取り上げたかったのですが、また別の機会に。