【次元削減】株価を二次元に埋め込んでみた(tsne,PCA,MDS)

こんにちは。ゴールデンウィーク２日目の日曜日の昼下がりです。データ解析をしつつ、外に出れない分どうぶつの森で散歩しています・・・
こちらが本日の記事の目次です。時間のない方は結果（差分化あり）だけご覧ください。次元圧縮すると米国株がセクターことにおおまかに分離できていることが分かります。また、対数差分化するとうまくいくというのが大きな収穫でした。

やりたいこと・モチベーション

さて今日は、株価のデータを対象に次元圧縮を用いた解析を行いたいと思います。私は米国株の運用を行っているのですが、企業の株の変動を見ていてあることに気が付きました。同じ分野（セクター）の企業の株価の推移はなんだか似ているんじゃないか？と。

具体例を見てみましょう。これは今年の２月までの工業セクターと公共事業セクターの一部企業の株価の推移をプロットしたものですが、工業セクターは2018年末に株価が暴落している傾向が程度の差はあれど見えると思います。一方で公共事業セクターは2018年末の株価暴落の影響が小さく、その後の株価変化率が上昇してるようにも見えます。このことから、株価の推移を多次元のベクトルと解釈し、これを次元圧縮して２次元のベクトルに特徴を埋め込むと、同じセクターの企業は近い領域にプロットされるだろう、と愚考した次第です。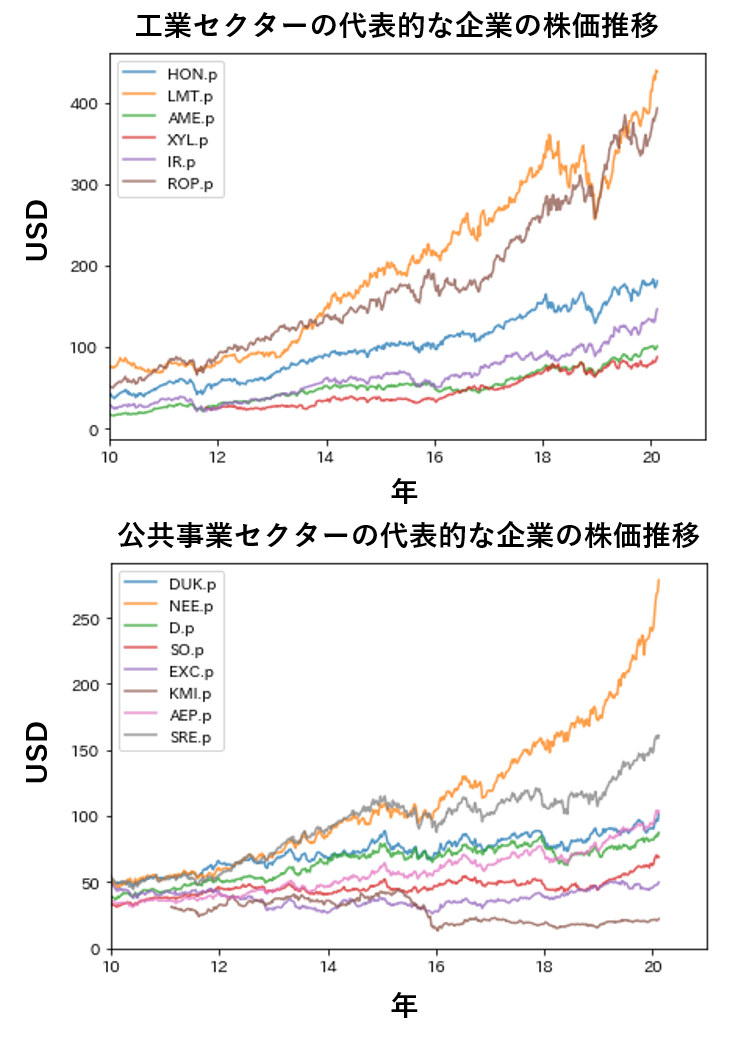

工業セクターと公共事業セクターの過去１０年間の株価推移。

解析対象

S&P500という経済指標に採用されている500企業の週ごとの株価推移の情報をスクレイピングによって取得しました（この方法はここで具体的に書きませんが、いつか記事にするかもしれません）。次元圧縮にはベクトルのサイズを合わせる必要がありますが、必ずしも各企業が同じサイズの時系列データを持っているわけではないので、現在から遡って600週（約11年）のデータを持っている約400企業を対象に絞りました。

コードと方法

次元圧縮はscikit-learnを用いると簡単に行うことができます。データの収集や前処理に手間がかかりますが、（学習データサイズ、株価ベクトルサイズ）の大きさの配列を生成すれば後は次元圧縮のコードを１行書くだけで実行できます。次元圧縮には複数の方法がありますが、ここでは主成分分析（PCA）、t分布型確率的近傍埋め込み法（t-sne）、多次元尺度構成法（MDS）を用いました。いずれも次元圧縮ではよく目にする手法です。

PCA

PCAは特異値分解という行列計算の手法を用いており、元データの次元をより分散の大きくなる軸に射影しています。これにより元データに含まれる情報を最大限活用するように次元が圧縮されます。またどの軸が最も情報を含んでいるかという寄与率が計算できることも特長の一つかと思います。
こちらの本が詳しいのでご興味のある方はご参照下さい。PCAに限らず、多変量解析の入門にはうってつけです。

多変量解析入門――線形から非線形へ

t-sne

t-sneはt分布を用いて次元圧縮する方法です。t分布は正規分布と比較して裾野の広い形状をしており、これを用いると似たデータがより近く、遠いデータがより遠く表現されるという特徴があります。詳しくはALBERT様の以下のブログ記事が大変詳しいため、そちらをご参照下さい。
blog.albert2005.co.jp

MDS

MDSはデータ間の距離を適当な尺度に基づいて計算し、得られた距離行列をもとに行列分解することによって次元を圧縮します。距離の尺度にはユークリッド距離やマンハッタン距離やコサイン距離など色々ありますが、scikit-learnはデフォルトでユークリッド距離に基づいた距離を計算しています。

データの差分化

株価情報はそのまま扱ってもよいのですが、株価の絶対値の大きさは同じ分野の企業であってもまちまちです。そのため変化の仕方が仮に似ていても絶対値が違いすぎると遠いベクトルとして処理されるリスクがあると考え、対数差分化を行いました。ちなみに対数差分化処理を施すと以下のような図が得られます。これはGOOGLE株の情報ですが、これだけ見ても人間にはなんのことやら、ですが意味があると信じてこれを次元圧縮しましょう。

GOOGL株の株価推移と対数差分化。

この時系列データ処理の方法は、以前のブログ記事でもまとめさせて頂きました。
dajiro.hatenablog.com

コードはこちらになりますが、元データがないのでこれをコピペしても動くことはないでしょう・・・。対数差分化の方法やscikit-learnでの次元圧縮の方法等の参考になればと思います。

import matplotlib.pyplot as plt
import japanize_matplotlib 
import pickle
import os
import numpy as np

from sklearn.decomposition import PCA
from sklearn.manifold import MDS, TSNE

f = pickle.load(open("../properties/SP500_table_new.pkl", "rb"))

for n, i in enumerate(f['セクター']):
    if i == ' エネルギー ':
        f['セクター'][n] = ' Energy '

colordict = {' Health Care ':"black", ' Consumer Discretionary ':"rosybrown",' Technology ':"orangered", ' Consumer Staples ':"orange", \
            ' Financials ':"yellowgreen", ' Utilities ':"lightseagreen", ' Materials ':"dodgerblue", ' Industrials ':"darkblue", \
            ' Energy ':"darkviolet", ' Communications ':"palevioletred"}

def makeArray(path):
    """ベクトルを標準化し次元圧縮用の配列を生成
    """
    dic = {}
    lst = []
    listdir = os.listdir(path)
    for ticker in listdir:
        with open(f'{path}/{ticker}', 'rb') as f:
            df = pickle.load(f)
        if len(df) > 600:
            #dic[ticker] = df['調整後終値'][-600:]
            #時系列の対数差分化処理
　　　　　　dic[ticker] = (1 + df.pct_change()['調整後終値']).apply(np.log)[-600:]
    
    arr = np.vstack([value for key, value in dic.items()])
    
    return arr, list(dic.keys())

#次元圧縮の対象となる配列を生成
arr, keys = makeArray('../update/2020_5_3_SP500/')

#３通りの次元圧縮方法で計算実行。たった１行！
X_reduced1 = PCA(n_components=2, random_state=0).fit_transform(arr)
X_reduced2 = TSNE(n_components=2, random_state=0).fit_transform(arr)
X_reduced3 = MDS(n_components=2, random_state=0).fit_transform(arr)

#結果の可視化
fig = plt.figure(figsize=(20, 8))
ax1 = fig.add_subplot(1, 3, 1)
ax1.scatter(X_reduced1[:, 0], X_reduced1[:, 1], s=0)
ax1.set_xlabel("X", fontsize=12)
ax1.set_ylabel("Y", fontsize=12)
ax1.set_title('PCA', fontsize=15)

ax2 = fig.add_subplot(1, 3, 2)
ax2.scatter(X_reduced2[:, 0], X_reduced2[:, 1], s=0)
ax2.set_xlabel("X", fontsize=12)
ax2.set_ylabel("Y", fontsize=12)
ax2.set_title('TSNE', fontsize=15)

ax3 = fig.add_subplot(1, 3, 3)
ax3.scatter(X_reduced3[:, 0], X_reduced3[:, 1], s=0)
ax3.set_xlabel("X", fontsize=12)
ax3.set_ylabel("Y", fontsize=12)
ax3.set_title('MDS', fontsize=15)

for idx, ticker in enumerate(keys):
    tic = ticker.replace('.p', '')
    ax1.annotate(f.at[tic, "セクター"], (X_reduced1[:, 0][idx], X_reduced1[:, 1][idx]), color=colordict[f.at[tic, "セクター"]], fontsize=10)
    ax2.annotate(f.at[tic, "セクター"], (X_reduced2[:, 0][idx], X_reduced2[:, 1][idx]), color=colordict[f.at[tic, "セクター"]], fontsize=10)
    ax3.annotate(f.at[tic, "セクター"], (X_reduced3[:, 0][idx], X_reduced3[:, 1][idx]), color=colordict[f.at[tic, "セクター"]], fontsize=10)

次元圧縮の結果（差分化なし）

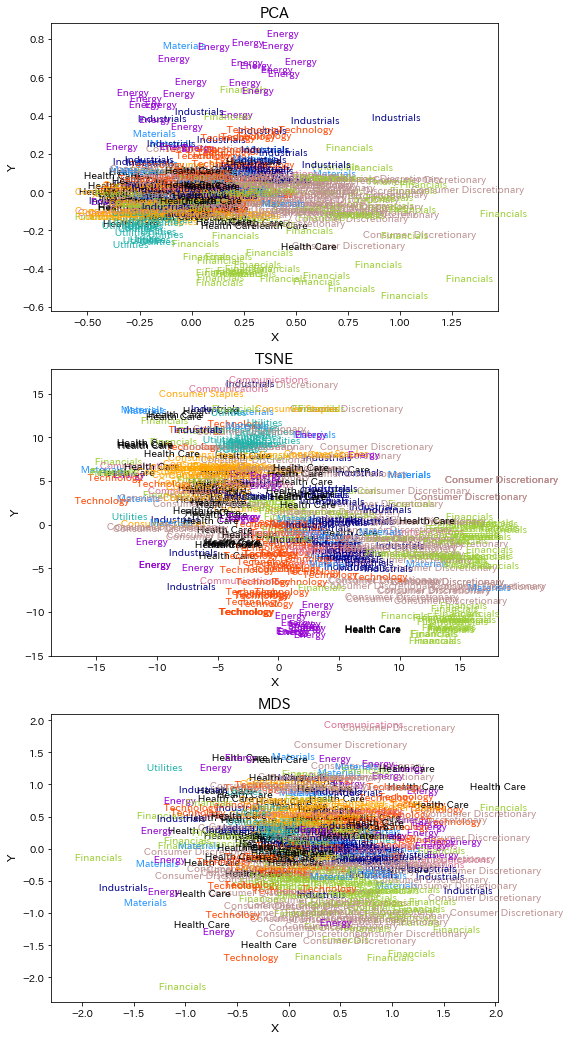
さっそくPCA、TSNE、MDSの結果を見てみましょう。次元圧縮した各点はその企業の分野（セクター）を表しており、セクターごとに色分けされています。株価の推移がセクターごとに似ている場合には、それぞれのセクターが固まって表示されます。しかしここでは差分処理をしておらず、はっきりとした傾向が見えません。同じセクターでも株価が非常に高いと株価のベクトルは決して近くはならないと思われるため、この結果は妥当であると思います。またPCA、MDSでは塊からかけ離れたデータが存在していますね。これらの正体はGOOGLEやAMAZON株であり、非常に高い株価のため遠くに配置されたのだと解釈できます。

差分化をしない状態での株価の次元圧縮の結果。

次元圧縮の結果（差分化あり）

では本命の対数差分化データの結果を見てみましょう。セクターごとにかたまっているように見えませんか？PCAでははっきりとEnergy(エネルギー、紫)セクター、financials（金融、緑）セクター、utility(小売り、水色)セクターのかたまりが見て取れます。またTSNEではTechnology（テクノロジー、赤）セクターやConsumer Stales(生活必需品、黄)セクター、industrials(工業、紺)セクターがかたまっています。MDSだとやや見づらいですが、こちらもセクターの塊を見て取ることができます。このことから、次元圧縮により代表的な米国株の株価動向がセクターごとに似通っていることが可視化されました！これをもとに株価予測を、などは難しいとは思いますが、次元圧縮や時系列データの対数差分化の威力がはっきり示された結果といえるのではないでしょうか。

対数差分化をしたあとに次元圧縮。セクターごとのかたまりが見える。